Nombre hexagonal

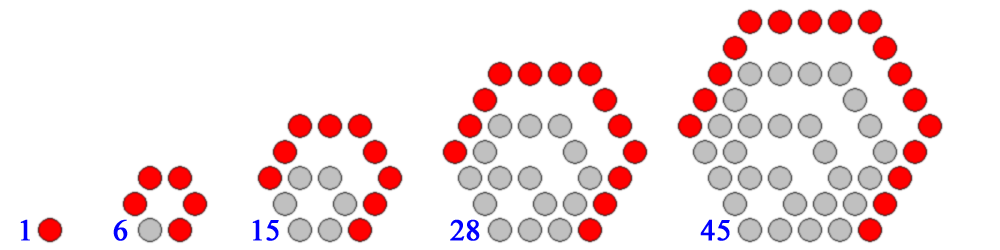
En mathématiques, un nombre hexagonal est un nombre figuré polygonal qui peut être représenté graphiquement par des points répartis dans un hexagone. Le nombre hexagonal d'ordre ${\displaystyle n}$ est donné par la formule ^, :

${\displaystyle H_{n}=P_{6,n}=n(2n-1)=P_{3,2n-1}}$.

Ainsi, les nombres hexagonaux sont simplement les nombres triangulaires d'indice impair.

Les vingt-deux premiers sont 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780, 861 et 946 (suite A000384 de l'OEIS).

Obtention de ces nombres

Pour avoir ${\displaystyle n}$ points sur chaque côté de l'hexagone extérieur, on ajoute à l'étape ${\displaystyle n}$ : ${\displaystyle 6-1}$ points aux sommets de l'hexagone et ${\displaystyle (6-2)(n-2)}$ points à l'intérieur des côtés, d'où ${\displaystyle H_{n}-H_{n-1}=5 4(n-2)=4(n-1) 1}$.

Donc ${\displaystyle H_{n}=\sum _{k=1}^{n}(4(k-1) 1)=\sum _{k=0}^{n-1}(4k 1)=2n(n-1) n=n(2n-1)}$.

Autre construction

De la formule générale ${\displaystyle P_{k,n}=P_{k-1,n} T_{n-1}}$, découle par exemple que ${\displaystyle H_{n}}$ est la somme du nombre carré d'ordre ${\displaystyle n}$ : ${\displaystyle C_{n}=P_{2,n}}$ et de deux nombres triangulaires d'ordre ${\displaystyle n}$ : ${\displaystyle H_{n}=C_{n} 2T_{n-1}=n^{2} n(n-1)}$  ; voir la figure de gauche, inscrivant cette construction dans un hexagone non régulier.

La figure de droite montre un hexagone, également non régulier, tracé dans un réseau carré, ce qui donne, pour l'étape ${\displaystyle n}$ où il y a ${\displaystyle n}$ points dans chaque côté : un rectangle de ${\displaystyle n(2n-1)}$ points et deux triangles de ${\displaystyle 1 3 \cdots 2n-3=(n-1)^{2}}$ points, soit ${\displaystyle n(2n-1) 2(n-1)^{2}=4n^{2}-5n 2}$ points, voir la suite A033951 de l'OEIS.

Propriétés

• ${\displaystyle H_{n}}$ est la somme du nombre triangulaire d'ordre ${\displaystyle n}$ et de trois nombres triangulaires d'ordre ${\displaystyle n-1}$ : ${\displaystyle H_{n}=T_{n} 3T_{n-1}}$.

• ${\displaystyle H_{n}=n 4T_{n-1}=n 2n(n-1)}$ est congru à ${\displaystyle n}$ modulo 4 et a donc même parité que lui.

• Réduite modulo 9, la suite des nombres hexagonaux suit périodiquement le motif des neuf valeurs suivantes : 1, 6, 6, 1, 0, 3, 1, 3, 0.

• Tout entier n > 130 peut être exprimé comme somme d'au plus quatre nombres hexagonaux ; Adrien-Marie Legendre l'avait démontré en 1830 pour n > 1791 (voir la suite A007527 de l'OEIS).

Références

Articles connexes

• Nombre polygonal
• Nombre hexagonal centré

• Arithmétique et théorie des nombres